TYPES OF ABSOLUTE MEASURES OF VARIATION
1. Range – is the difference between the highest score and the lowest score in a
distribution.
a. Range for Ungrouped Data
Formula: R= HS-LS
Where: R – range value
Where: R – range value
HS – highest score
LS – lowest score
Example 1
|
Group A
|
Group B
|
|
10(LS)
12
15
17
25
26
28
20
35(HS)
|
15(LS)
16
16
17
17
23
25
26
30(HS)
|
R= HS-LS
R=35-10
R= 25
b. Range for Grouped Data
Formula: R= HSUB – LSLB
Where: R- range value
HSUB – upper boundary of the highest score
LSLB– lower boundary of the lowest score
Example 2 :Find the value of range of the scores of 50 students in Mathematics achievement test.
X
|
F
|
25-32
|
3
|
33-40
|
7
|
41-48
|
5
|
49-56
|
4
|
57-64
|
12
|
65-72
|
6
|
73-80
|
8
|
81-88
|
3
|
89-97
|
2
|
N= 5
|
Solution:
LL of the LS = 25
LSLB – 24.5
LSLB – 24.5
UL of the HS – 97
HSUB = 97.5
R= HSUB – LSLB
R= 97.5-24.5
R= 73
Properties of Range:
1. It is quick and easy to understand.
2. It is a rough estimation of variation.
3. It is easily affected by the extreme scores.
Interpretation of the range Value:
When the range value is large, the scores in the distribution are more dispersed, widespread or heterogeneous. On the other hand, when the range value is small the scores in the distribution are less dispersed, less scattered or homogeneous.
2. Inter-quartile range (IQR) and Quartile Deviation (QD)
Inter-quartile Range – is the difference between the third quartile and the first quartile.
IQR=Q3-Q1
Properties of Inter-quartile Range
1. Reduces the influence of extreme values.
2. Not as easy as to calculate as the range.
3. Only considers the middle 50% of the scores in the distribution.
4. The point of dispersion is the median value.
Quartile Deviation – indicates the distance we need to go above the median to include the middle 50% of the scores.
Formula: QD= Q3-Q1
2
Steps in Solving Quartile Range:
· Solve for the value of Q1.
· Solve for the value ofQ3.
· Solve for the value of QD using the formula QD= Q3-Q1
A. Quartile Deviation for Ungrouped Data
Example:
x(scores)
6
8
10
12
12
14
15
16
20
|
Solve for the Q1: Solve for Q3:
N=9 Q3= [ ¾ n + (1- ¾) ]
Q1 = [¼ n + (1 – ¼)] = [ ¾ (9) +(1- ¾) ]
= [¼ (9) + (1 – ¼)] = [ 27/4 + ¼ ]
= [ 9/4 + ¾] = [28/4]
= [12/4] = 7th score
= 3rd score = 15
= 10
IQR = Q3-Q1 QD = Q3-Q1
= 15-10 2
= 5 = 15-10
2
= 5/2
QD = 2.5
B. QUARTILE DEVIATION OF GROUPED DATA
QD= Q3-Q1
2
Example:
x
|
f
|
Cf<
|
25-32
|
3
|
3
|
33-40
|
7
|
10
|
41-48
|
5
|
15
|
49-56
|
4
|
19
|
57-64
|
12
|
31
|
65-72
|
6
|
37
|
73-80
|
8
|
45
|
81-88
|
3
|
48
|
89-97
|
2
|
50
|
N=50
|
Solve for the value of Q1.
n/4 = 50/4 =12.5
Q1C = 41 – 48
LL = 41
LB = 40.5
Cfp = 10
Cfp = 10
Fq = 5
c.i = 8



Interpretation of IQR and QD
The larger the value of the IQR or QD, the more dispersed the scores at the middle 50% of the distribution. On the other hand, if the IQR or QD is small, the scores are less dispersed at the middle 50% of the distribution. The point of dispersion is the median value.
3. Mean deviation – measures the average deviation of the values from the arithmetic mean.
a. MEAN DEVIATION FOR UNGROUPED DATA
Where:
MD = mean deviation value
X = individual score
x = sample mean
n = number of class
Steps in solving Mean Deviation for ungrouped Data:
1. Solve for the mean value.
2. Subtract the mean value from each score.
3. Take the absolute value of the difference in step2.
4. Solve for the mean deviation using the formula.
a. MEAN DEVIATION FOR GROUPED DATA
Where:
MD = mean deviation value
f = class frequency
xm = class mark or midpoint
n = number of class
Steps in solving Mean Deviation for Grouped Data:
1. Solve for the value of mean.
2. Subtract the mean value from each midpoint or class mark.
3. Take the absolute value of each difference.
4. Multiply the absolute value and the corresponding class frequency.
5. Find the sum of the results in step 4.
6. Solve for the mean deviation using the formula.
 |
Analysis:
The mean deviation of the 40 scores of students is 10.63. this means that on the average, the value deviated from the mean of 33.63 is 10.63.
4. Variance and the Standard Deviation
Variance - one of the most important measures in variation.
Steps in solving Variance for Ungrouped Data:
1. Solve for the mean value.
2. Subtract the mean value from each score.
3. Square the difference between the mean and each score.
4. Find the sum of the results in step3.
5. Solve for the population variance or sample variance using the formula of ungrouped data.
a. Variance for Ungrouped Data
b. Variance of Grouped Data
Note: If the standard deviation is already solved, square the value of the standard deviation to get the variance.
Steps in solving Variance of Grouped Data:
1. Solve for the mean value.
2. Subtract the mean value from each midpoint or class mark.
3. Square the difference between the mean value and midpoint or class mark.
4. Multiply the squared difference and the corresponding class frequency.
5. Find the sum of the step 4.
6. Solve for the population variance or sample variance using the formula.
Standard Deviation – is the most important measures in variation. It is also known as the square root of the variance. It is the average distance of all the scores that deviates from the mean value.
Population Standard Deviation
Sample Standard Deviation
RELATIVE MEASURE of VARIATION:
Coefficient of Variation – shows variation relative to the mean. It is used to compare two or more groups of distribution of scores.
Formula:
REFLECTION:
Not all distribution of scores can be measured by just using the central tendency because central tendency does not actually describe distribution. But, with the help of variation, spread of scores are easily described.

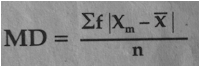



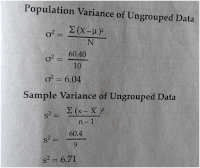






No comments:
Post a Comment